排序算法

冒泡排序
选择排序
插入排序
快速排序
合并排序
分治法

冒泡排序

思路：从数组开头开始，将未被排序的数组元素排序，然后迭代数组。该方法通过比较相邻元素然后置换元素完成排序。就是遍历数组，直到整个数组没有可交换元素为止。
时间复杂度 O(n^2)，空间复杂度 O(1)

//冒泡排序
function bubbleSort(array) {
  var len = arr.length;
  for (var i = 0; i < len-1; i++) {
    for (var j = 0; j < len - 1 - i; j++) {
        // 相邻元素两两对比，元素交换，大的元素交换到后面
        if (arr[j] > arr[j + 1]) {
            var temp = arr[j];
            arr[j] = arr[j+1];
            arr[j+1] = temp;
        }
    }
  }
}

选择排序

思路：通过选择列表中最小值来与列表中第一个值进行对比交换，然后从第二个位置逐一对比，选择剩下列表中最小值来与第二个值交换位置。然后循环遍历列表并交换元素，直到最后一个元素为止。
所有情况均为时间复杂度 O(n^2),空间复杂度 O(1)

//选择排序
function selectionSort(array){
  const len = array.length;
  var minIndex,temp;
  for(let i=0;i<len-1;i++){
    minIndex = i;
    for(let j=i+1;j<len;j++){  //找到最小值下标
      if(array[j]<array[minIndex]){
        minIndex = j;
      }
    }
    temp = array[i];
    array[i] = array[minIndex];
    array[minIndex] = temp;
  }
}

插入排序

思路：通过在列表的开头建一个排序的数组来实现整个排序，它以第一个元素开始排序数组，然后检查对比下一个元素，并将其向后交换到排序的数中，直到它处在排序的位置。循环迭代整个列表，将新产生的元素交换到排序部分，直到整个列表处于排序状态。该算法在平均和最坏的情况下时间复杂度 O(n^2)

//插入排序
function insertionSort(array){
  let len = array.length;
  let preIndex, current;
  for (let i = 1; i < len; i++) {
    preIndex = i - 1;
    current = array[i];   //第一轮从array[1]开始向前比较
    while (preIndex >= 0 && current < array[preIndex]) {
      array[preIndex + 1] = array[preIndex];  //向后交换元素
      preIndex--;
    }
    array[preIndex + 1] = current; //将要排序的元素交换到正确排序位置
  }
}

快速排序（常见）

快速排序采用分治法
思路：将原始数组选择一个基准值(下面的算法以中间数为基准)，将数组划分为两个子数组，其值大于或者小于基准值。然后两个子数组分别递归调用此快排算法排序，直到为空数组和单个元素数组的情况，得到结果。
平均时间复杂度：O(nlogn)
空间复杂度 O(logn)(基准元素储存空间)

//快速排序（以区间第一个数为基准）  例如：[2,6,3,8,1,9]
function quickSort(arr, l ,r){
  if(l<r){
    var i=l, j=r, x=arr[l];  //以区间第一个数为基准(挖第一个坑）  x=a[0]=2 [_,6,3,8,1,9]
    while(i<j){
        while(i<j && arr[j]>=x){  //从右边向左找第一个小于基准的数   arr[4]=1 （挖新坑） [_,6,3,8,_,9]
            j--;
        }
        arr[i] = arr[j];  //填上一个（第一个）坑  [1,6,3,8,_,9]
        while(i<j && arr[i]<x){  //从左向右找第一个大于或者等于基准的数 （挖新坑）a[1]=6  [1,_,3,8,_,9]
            i++;
        }
        arr[j] = arr[i];  //填上一个坑 [1,_,3,8,6,9]
    }
    arr[i] = x;  //退出时，i等于j。将x填到最后这个坑中 [1,2,3,8,6,9]
    quickSort(arr, l, i);  //递归左数组
    quickSort(arr, i+1, r);  //递归右数组
  }
  return arr;
}

若以其他元素为基准，只需要最开始将基础元素与最左边元素交换即可

合并排序（常见）

思路：也采用了分而治之的递归方法来排序数组。利用递归将数组一分为二，直到数组里面只包含一个元素为止。单个元素的数组是自然序的，然后合并生成一个最终的排序数组。
合并排序是一种高效的排序方式时间复杂度：O(nlogn)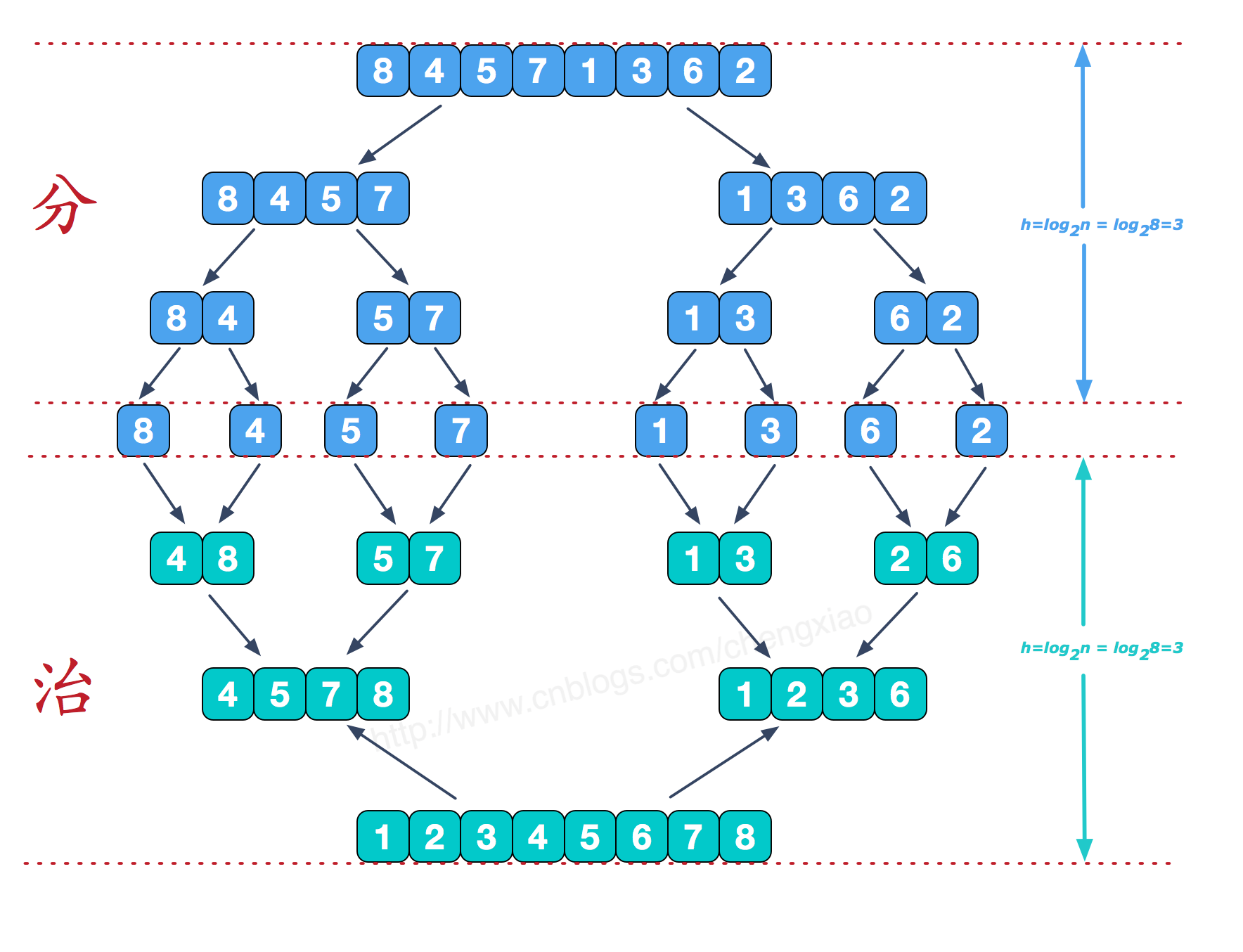

具体的实现过程如下：

//合并排序（自上而下的递归）
function mergeSort(array) {
  if(array.length<2){
    return array;
  }
  var mid = Math.floor(array.length/2);
  var left = array.slice(0,mid);     // slice(start,end)返回数组指定元素的新的数组
  var right = array.slice(mid);
  return merge(mergeSort(left),mergeSort(right));
}

function merge(left, right){   //合并
  var result = [];
  while(left.length && right.length){
    if(left[0]<=right[0]){
      result.push(left.shift());   //shift():删除数组第一个元素，并返回删除元素的值
    }else{
      result.push(right.shift());
    }
  }
  while(left.length){
    result.push(left.shift());
  }
  while(right.length){
    result.push(right.shift());
  }
  return result;
}